Problem Set 2
Investment Theory
Instructions: This problem set is due on 9/12 at 11:59 pm CST and is an individual assignment. All problems must be handwritten. Scan your work and submit a PDF file.
Problem 1 You have a logarithmic utility function \(u(W) = \ln W,\) and your current level of wealth is $5,000.
- Imagine you are in a situation where there’s a 50/50 chance of either winning or losing $1,000. You have the option to purchase insurance for $125 that would entirely eliminate this risk. Would you choose to buy the insurance or take the gamble?
- Let’s say you chose to take the gamble in part (a) and ended up losing, which reduces your wealth to $4,000. Now, if you are presented with the same gamble and the same insurance offer of $125, would you opt to buy the insurance this time?
Problem 2 An entrepreneur faces the following risks: a 10% chance that a fire will reduce her net worth to $1, a 10% chance that a fire will lower it to $50,000, and an 80% chance that nothing will happen, maintaining the business’s value at $100,000. Her utility function is logarithmic, given by \(u(W) = \ln W.\) She is considering an insurance policy that would provide a payout of $99,999 in the first scenario, $50,000 in the second, and nothing in the third. What is the maximum amount she would be willing to pay for this insurance policy?
Problem 3 Consider gamble \(A\):
| Gain | Probability |
|---|---|
| -2 | 0.09 |
| 4 | 0.30 |
| 10 | 0.40 |
| 16 | 0.21 |
From \(A\), we can construct another gamble \(B\) by adding white noise to a number of outcomes. Indeed, we can replace the outcome 4 in gamble \(A\) by the gamble \(A'\):
- 3 with probability 1/2
- 5 with probability 1/2
with \(\ev(A') = 4\). In the same manner, we can replace outcome 16 in gamble \(A\) with gamble \(A''\):
- 12 with probability 1/3
- 18 with probability 2/3
with \(\ev(A'') = 16.\)
Explain why any risk averse individual would prefer gamble \(A\) to gamble \(B.\)
Problem 4 Consider the following information about a risky portfolio that you manage, and a risk-free asset: \(\mu_{Q} = 11\%\), \(\sigma_{Q} = 15\%\), \(r_{f} = 5\%\).
- Your client wants to invest a proportion of her total investment budget in your risky fund to provide an expected rate of return on her overall or complete portfolio equal to 8%. What proportion should she invest in the risky portfolio, \(P\), and what proportion in the risk-free asset?
- What will be the standard deviation of the rate of return on her portfolio?
- Another client wants the highest return possible subject to the constraint that you limit his standard deviation to be no more than 12%. Which client is more risk averse?
Problem 5 Assume that you manage a risky portfolio with an expected rate of return of 18% and a standard deviation of 28%. The T-bill rate is 8%. Your client’s degree of risk aversion is \(A = 3.5\), assuming a utility function \(U = \mu - 0.5 A \sigma^2\).
- What proportion of the total investment should be invested in your fund?
- What is the expected return on your client’s optimized portfolio?
- What is the standard deviation on your client’s optimized portfolio?
Problem 6 Consider the following graph that plots four indifference curves of an investor with utility score given by \(U = \mu - 0.5 A \sigma^{2}.\)
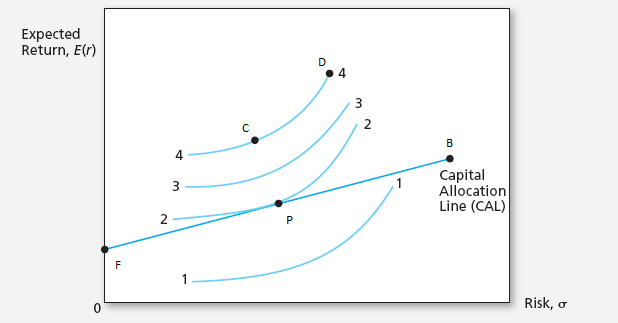
Currently, the investor can only invest in the risk-free asset denoted by \(F\), and a risky asset denoted by \(B\). You know that \(\mu_{B} = 11\%,\) \(\sigma_{B} = 15\%,\) and that the risk-free asset yields 5%.
- Which indifference curve (1, 2, 3, or 4) represents the greatest level of utility that can be achieved by the investor? Why?
- For which value of the risk-aversion coefficient would the optimal portfolio chosen by the investor be composed of 50% in the risky asset?
Problem 7 Assume that you manage a risky portfolio with an expected rate of return of 18% and a standard deviation of 28%. The T-bill rate is 8%. Your client chooses to invest 70% of a portfolio in your fund and 30% in a T-bill money market fund.
What is the expected value and standard deviation of the rate of return on his portfolio?
Suppose that your risky portfolio includes the following investments in the given proportions:
Asset Proportions Stock A 25% Stock B 32% Stock C 43% What are the investment proportions of your client’s overall portfolio, including the position in T-bills?
What is the reward-to-volatility ratio, i.e. the Sharpe ratio, of your risky portfolio and your client’s portfolio?
Problem 8 Investment Management Inc. (IMI) uses the capital market line to make asset allocation recommendations. IMI derives the following forecasts:
- Expected return on the market portfolio: 12%.
- Standard deviation on the market portfolio: 20%.
- Risk-free rate: 5%.
Samuel Johnson seeks IMI’s advice for a portfolio asset allocation. Johnson informs IMI that he wants the standard deviation of the portfolio to equal half of the standard deviation for the market portfolio. Using the capital market line, what expected return can IMI provide subject to Johnson’s risk constraint?
Problem 9 Suppose that you have $1 million and the following two opportunities from which to construct a portfolio:
- Risk-free asset earning 12% per year.
- Risky asset with expected return of 30% per year and standard deviation of 40%.
If you construct a portfolio with a standard deviation of 30%, what is its expected rate of return?